n e 
0,...,d 
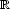, tali che
0 + 
+ d = 1. Il punto
Siano dati p0,...,pd n e
0,...,d 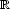, tali che
0 + + d = 1. Il punto
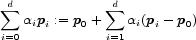 | (1) |
è detto una combinazione affine dei punti p0,...,pd.
L’insieme di tutte le combinazioni affini di {p0,...,pd}è un sottospazio affine detto guscio affine di tali punti, e denotato come aff {p0,...,pd}. È facile verificare che:
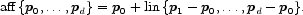
La dimensione di un sottospazio affine è la dimensione
dello spazio vettoriale corrispondente. Sottospazi affini di
d con dimensioni 0, 1, 2 e d - 1 sono detti punti, linee,
piani e iperspazi, rispettivamente. I sottospazi affini sono
detti anche insiemi piatti (“flats”).
Ogni sottospazio affine può essere descritto sia come intersezione di iperpiani affini, sia come guscio affine di un insieme finito di punti.